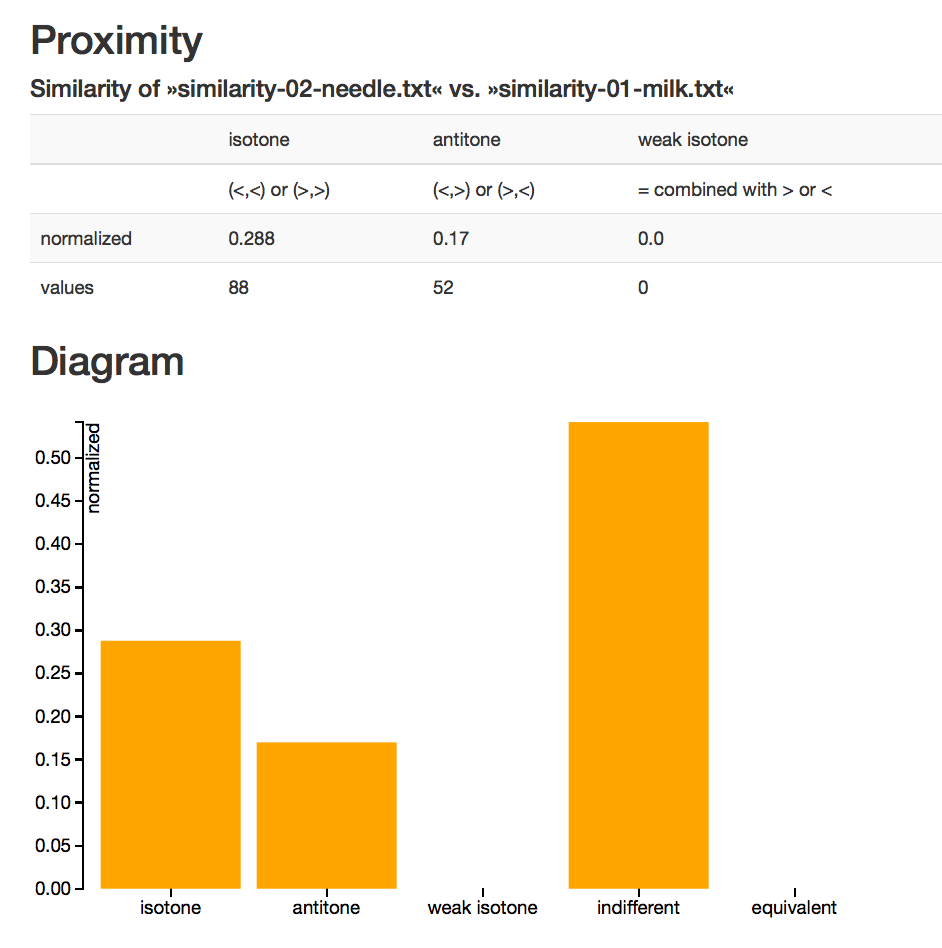
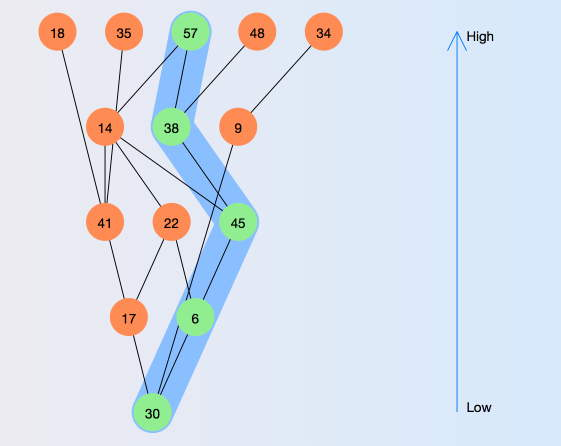
(March 2015)
The module spyout, is thought of as an introductory program, making newcomers
familiar with some ideas of the theory of partially ordered sets. The module
spyout should at best motivate the user to try out the other already existing
modules.
The module spyout has as usual:
Basic information concerning the data matrix (Menue: “Calculate”):
- list of objects
- list of attributes (indicators)
- output of the data matrix
and both important order theoretical matrices the zeta-matrix as well as the
cover-matrix.
It informs about equivalence classes and its representative elements.
Furthermore a Hasse diagram can be obtained with all its facilities (zooming,
downsets, upsets, local Hasse diagram incomparables).
So far, spyout provides the same basic information pieces as any other module
of PyHasse.
Specifically spyout informs about (Menue “Show”):
Basic statistics of the data matrix for each indicator: When the user want
to get more information in that context, other software products could be
helpful, for example the free software R.
Connectivities: Here a list appears, where for each representative
element x the number of elements in the
- down set
- upset
- appears together with the number
of elements incomparable with x
Chain list
A connectivity between x and an element z for instance in the down set does not
necessarily mean that there is only one path from x to z. Therefore the next
step could be to check “chain list”, where all chains are listed, which are
possible between x and z, ordered due to decreasing length. A more extensive
study of chains can be the next step, especially following the question
whether or not chains of the same length are similar. This question can be
studied in the module chain.
Conflicts
No connection between x and an element y: Then y is one of the elements in the
set of elements incomparable with x. Then a further study is possible to find
out, what are the reasons for the incomparability in terms of the indicator
values. I.e. here the the submenu “conflicts” can be helpful. When still more
information is wanted then the module acm can be helpful.
Have a look at the documentation
and/or calculation of the module.